The Nature of Sound
Intensity and Loudness of Sound
A friend whispers to you in a voice so soft that she has to lean very close so you can hear what she’s saying. Later that day, your friend shouts to you from across the room. Now her voice is loud enough for you to hear her clearly even though she’s several meters away. Obviously, sounds can vary in loudness.
It’s All About Energy
Loudness refers to how loud or soft a sound seems to a listener. The loudness of sound is determined, in turn, by the intensity of the sound waves. Intensity is a measure of the amount of energy in sound waves. The unit of intensity is the decibel (dB).
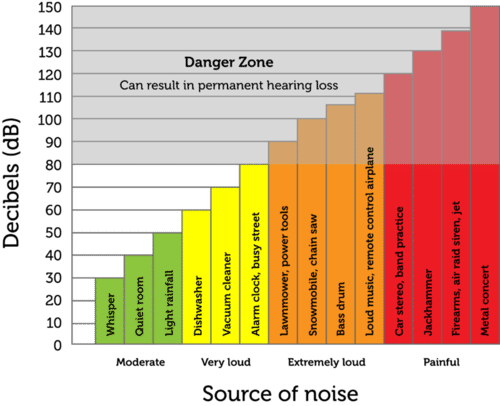
Decibel Levels
The Figure below shows decibel levels of several different sounds. As decibel levels get higher, sound waves have greater intensity and sounds are louder. For every 10-decibel increase in the intensity of sound, loudness is 10 times greater. Therefore, a 30-decibel “quiet” room is 10 times louder than a 20-decibel whisper, and a 40-decibel light rainfall is 100 times louder than the whisper. High-decibel sounds are dangerous. They can damage the ears and cause loss of hearing.
Amplitude versus Distance
The intensity of sound waves determines the loudness of sounds, but what determines intensity? Intensity results from two factors: the amplitude of the sound waves and how far they have traveled from the source of the sound.
Amplitude is a measure of the size of sound waves. It depends on the amount of energy that started the waves. Greater amplitude waves have more energy and greater intensity, so they sound louder.
As sound waves travel farther from their source, the more spread out their energy becomes. You can see how this works in the Figure below. As distance from the sound source increases, the area covered by the sound waves increases. The same amount of energy is spread over a greater area, so the intensity and loudness of the sound is less. This explains why even loud sounds fade away as you move farther from the source.
This diagram represents just a small section of the total area of sound waves spreading out from a source. Sound waves actually travel away from the source in all directions.
Inverse Square Law
Sound decreases 6 dB every time the distance is doubled. The Inverse Square Law states that as the distance doubles: The dispersing of a single source spreads over four times the area becoming only ¼ of its intensity. Each factor of two in distance from the source leads to a decrease in intensity by a factor of four.
The factor of four decrease in a wave's intensity is equivalent to a decrease of six decibels, so that a spherical wave attenuates at a rate of six decibels for each factor of two increase in distance from the source.
If you know the sound level at a point ‘x’ meters from the source, sound level can be calculated at any other distance with the help of the calculator below:
Adding two sources of Sound.
Sound pressure levels are expressed in decibels, which is a logarithmic scale. Therefore we cannot simply arithmetically add noise levels. For example, 35 dB plus 35 dB does not equal 70 dB.
To add two or more noise levels, if the difference between the highest and next highest noise level is:
0–1 dB then add 3 dB to the higher level to give the total noise level
2–3 dB then add 2 dB to the higher level to give the total noise level
4–9 dB then add 1 dB to the higher level to give the total noise level
10 dB and over, then the noise level is unchanged (i.e. the higher level is the total level)
So, 35 dB + 35 dB = 38 dB; 35 dB + 38 dB = 40 dB; 35 dB + 40 dB = 41 dB & 35 dB + 45 dB = 45 dB.